According to Wikipedia, a Ford circle is a circle with center at (p/q, 1/(2q^2)) and radius 1/(2q^2), where p/q is an irreducible fraction, i.e. p and q are coprime integers.
There is an interesting connection between the Farey sequence and Ford circles. The following graphic is based on the simple algorithm found in the Wikipedia Faray sequence entry. More information about Ford circles can be found at Mathworld.
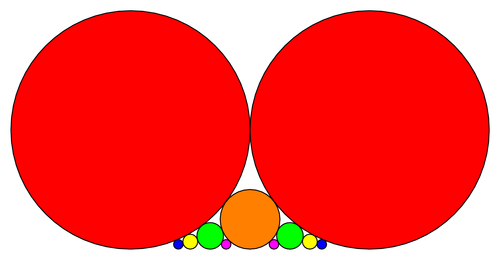
% Wikipedia : In mathematics, a Ford circle is a circle with centre at (p/q, 1/(2q^2)) and
% radius 1/(2q^2), where p/q is an irreducible fraction, i.e. p and q are coprime
% integers.
% There is an interesting connection between Farey sequence and Ford circles.
% The following graphic is based on the Simple algorithm that you can find here
% http://en.wikipedia.org/wiki/Farey_sequence
% interesting information can be found here
% http://mathworld.wolfram.com/FordCircle.html
\documentclass{article}
\usepackage[dvipsnames]{xcolor}
\usepackage{tikz}
\newcommand{\drawcircle}[3]{%
\pgfmathparse{1/(2*#2*#2)}
\let\tempradius\pgfmathresult
\draw[fill=#3] (#1/#2,\tempradius) circle (\tempradius);
}
\begin{document}
\def\fordN{5}
\def\fordA{0}
\def\fordB{1}
\def\fordC{1}
\let\fordD\fordN
\begin{center}\begin{tikzpicture}[scale=4]
\drawcircle{\fordA}{\fordB}{red}
\foreach \i/\c in
{0/blue,1/yellow,2/green,3/magenta,
4/orange,5/magenta,6/green,7/yellow,8/blue,9/red}{%
\pgfmathparse{\fordN+\fordB}\global\let\fordK\pgfmathresult
\pgfmathparse{floor(\fordK/\fordD)}\global\let\fordK\pgfmathresult
\pgfmathparse{\fordK*\fordC}\global\let\fordE\pgfmathresult
\pgfmathparse{\fordE-\fordA}\global\let\fordE\pgfmathresult
\pgfmathparse{\fordK*\fordD}\global\let\fordF\pgfmathresult
\pgfmathparse{\fordF-\fordB}\global\let\fordF\pgfmathresult
\global\let\fordA\fordC
\global\let\fordB\fordD
\global\let\fordC\fordE
\global\let\fordD\fordF
\drawcircle{\fordA}{\fordB}{\c}
}
\end{tikzpicture}\end{center}
\end{document}
% name Ford Circle
% utf8
% pdflatex
% author Alain Matthes
Source: TeXample.net