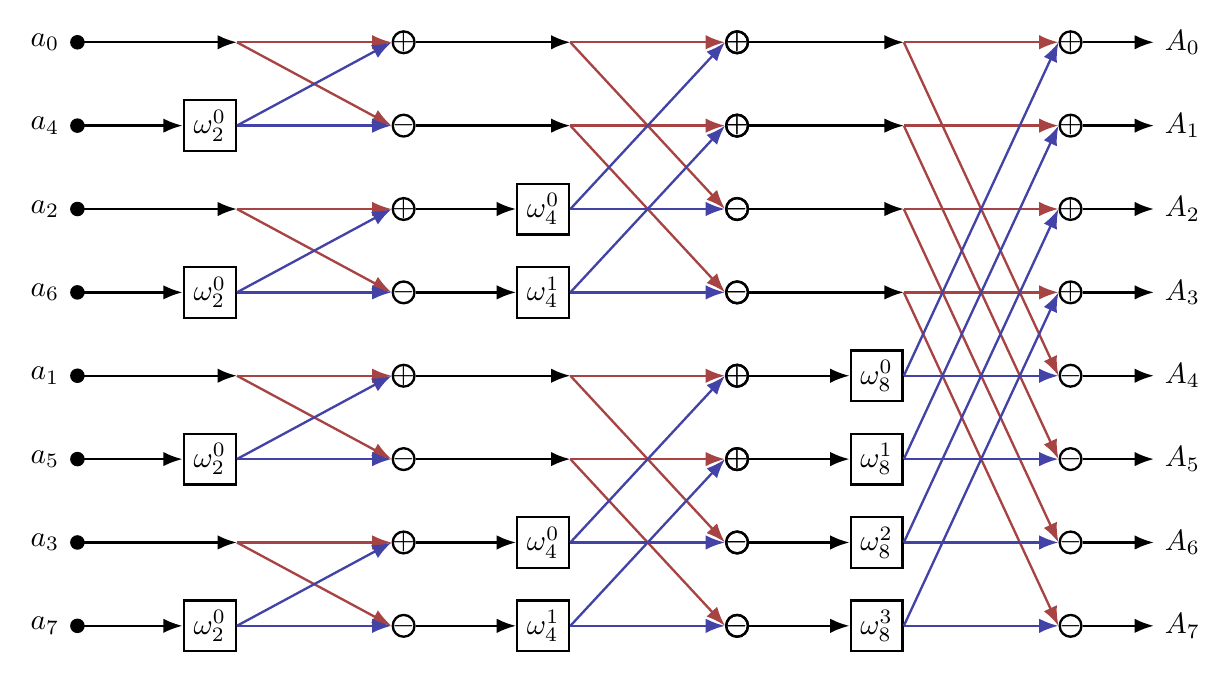
Schéma explicatif de la transformation de Fourier rapide

Schéma explicatif de la FFT pour une suite de 2^3=8 valeurs, et donc de 3 étages

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
\documentclass[border=10pt]{standalone}
\usepackage{tikz,ifthen}
\newcounter{ym}
\newcounter{yp}
\newcounter{ai}
\newcounter{wi}
\definecolor{myblue}{RGB}{67,67,167}
\definecolor{myred}{RGB}{167,67,67}
\usetikzlibrary {arrows.meta}
\begin{document}
\tikzstyle{n}= [circle, fill, minimum size=4pt,inner sep=0pt, outer sep=0pt]
\tikzstyle{mul} = [circle,draw,inner sep=-1pt]
\begin{tikzpicture}[>=Latex,thick]
  \foreach \y in {0,...,7}
  \coordinate
  (N-0-\y) at (0,-\y);
  \node[left] at (N-0-0) {$a_0$};
  \node[left] at (N-0-1) {$a_4$};
  \node[left] at (N-0-2) {$a_2$};
  \node[left] at (N-0-3) {$a_6$};
  \node[left] at (N-0-4) {$a_1$};
  \node[left] at (N-0-5) {$a_5$};
  \node[left] at (N-0-6) {$a_3$};
  \node[left] at (N-0-7) {$a_7$};
  \foreach \y in {0,...,7}
  {
    \ifodd\y
    \node[draw,anchor=east]
    (N-1-\y) at (2,-\y) {$\omega_{2}^0$};
    \else
    \coordinate
    (N-1-\y) at (2,-\y);
    \fi
    \draw[{Circle[]}->] (N-0-\y.east)--(N-1-\y.west);
  }
  \foreach \y in {0,...,7}
  {
    \ifodd\y
 
 
הההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההההה
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX